读《GEB》
哥德尔、艾舍尔、巴赫三块稀世瑰宝嵌为一体,集异壁之大成
一 WU谜题
——三部创意曲
规则如下:
- 如果一个归你所有的符号串的结尾是J,则可以在后面再加上一个U
- 如果你有Wx,那么可以得到Wxx
例:
从WJU可以得到WJUJU
从WU可以得到WUU
- 如果字符串中出现JJJ,可以用U替代
例:
从WJJJJ,可以得到WUJ和WJU
- 如果出现UU可以去掉
例:
UUU得到U
WUUUJJJ得到WUJJ
问:
能够通过如上规则从WJ推出WU吗?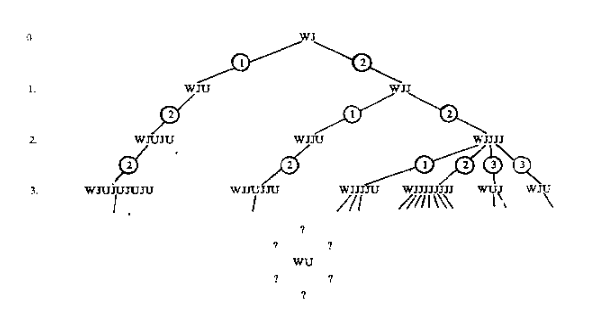
书摘
一个很不聪明的人,也会禁不住观察他自己在做什么,这些观察给予他关于所做的这项工作的洞察力,而计算机程序则缺乏洞察力。
无论用了多久,无论多好的车,也永远不会有躲避道路上的其他汽车或障碍物的能力,永远不会知道它的主人常走的路线(距离作者写下这段话大约过了40余年的今日,自动驾驶至少已经走得远超作者的想象了)
二 数学中的意义与形式
——二部创意曲
当你遇到一个你一无所知的形式系统,并且假如你希望去发现它的某种隐藏的含义,你的问题就在于给它的符号赋予一种有意义的解释。
当数学家发现在他所知的两个结构中间存在同构关系时,就会感到很愉悦。正是这种同构的认识在人的头脑中创造了意义。
形式系统中的符号虽然一开始没有意义,但至少在发现同构关系中,不可避免地会带上某种意义。
我们那些所给出地用于符号处理地规则,是否真的与我们通常地心理推理能力相等。或者更一般地说,用某种形式系统来表达我们思维能力地水平,在理论上是否有可能。
三 图形与衬底
——无伴奏的阿基里斯鸣奏曲
印符操作
- 读入并认出有限的符号集合中任何一个符号
- 写下属于该集合的任何一个符号
- 把任何一些那样的符号从一处复制到另一处
- 删除任何一些那样的符号
- 检测一个符号是否和另一个符号相等
- 保存并使用一列以前产生的定理
J方式工作者只是机械地,快乐地遵循规则,从不产生疑问
W工作者会趋于把符号串和对符号串地理解相混淆
U工作者是禅宗,拥抱一致性与不一致性
公理:简单、公平、一目了然了用不着去证明的、大家都公认可的理论。
定理:不能一目了然的表达让大家公认,必须借助公理或逻辑 表达后才能让大家肯定的理论结论。
四 一致性、完全性与几何学
——对位藏头诗
法卡斯真是一个浪漫的人啊
对话既有显明的意义也有隐含的意义
什么是音乐呢?是空气中的一系列震颤,还是大脑中相继的情感反应? 都是
哥德尔定理转述到唱机中:对任何一个唱机,都有它不能播放的唱片,因为后者会导致前者共振进而间接自摧毁。
哥德尔似乎发掘出了以前不被人知,但却意味深长的人类推理与机械推理之间的区别。这种生命系统的能力和无生命系统的能力间的差异,在真理概念与定理资格之间的差异上反映了出来。
欧几里得的《几何原理》用来构建的东西是人类的语言,一种充满隐患的复杂又难以捉摸的媒介。(语言的定义总是不那么精确,一个词的意思定义的范围常常不够精确)
欧几里得五公设:
- 一条直线段可以联接两个点
- 一条直线段上任何一条直线可以无限延伸
- 给定一条直线段,可以一个端点为圆心,以此线段为半径做一个圆
- 一切直角都彼此相等
- 如果两条直线与第三条直线相交时,在第三条直线的某一侧三条线所夹得内角和小于两个直角之和,则这两条直线沿着这一侧延伸足够长之后必然相交。
第五公设不如前四个那么美好,这条公设的被推翻导致了非欧几何被认可,一个真正的几何学新品种。
1823年非欧被两个人同时发现,匈牙利数学家雅诺.鲍耶,21岁;俄国数学家尼古拉斯.罗巴切夫斯基,30岁。
鲍耶的父亲法卡斯.鲍耶是高斯的密友,投入了大量精力去证明欧几里得第五公设,在给儿子的信中,他努力劝儿子不要思考这种东西:
原文如下
当一个人彻底离开生活的琐碎,他就转向了崇高之最,当我看出没有人能达到黑夜的尽头时,我转身回头了……我旅经了这地狱般的死海里所有的暗礁,总是帆破桅折地回来,就是从那时起,我开始衰老了,性情也毁了。我不加思索地用我的生命和幸福去冒险——或者光荣如凯撒,或者一无所有。
若你能使自己摆脱那些先入的印象,只让“直线”是那种满足新命题的产物,那你就达到一个崭新的境界。
重看第五公设,设置一个否定公设,称为平行公设
给定任意一直线和一个不在直线上的点,存在有且仅有一条通过那个点,且永不与前一条直线相交的直线,无论两直线延伸多远。
如果断言没有这样的直线,你就得到了椭圆几何学,如何断言至少有两条直线,你就得到了双曲几何学
一致性是说:”系统产生的每一个东西都是真的“,完全性是倒过来:”每一个真陈述都是由系统产生的“
五 递归结构和递归过程
——和声小迷宫
阿基里德想对着神灯许愿,“我要一百个愿望”,精灵说,“我需要向元精灵和造物神申请,因为你提出的是一个元愿望”
堕界:没有打出的嗝和已经熄灭的灯光所在的地方,它是一种侯室,在这里处于休眠状态的软件等着宿主回来。
作曲家运用他的和声进行来控制你的感情,使你产生渴望听到主调音的愿望。
尽管底层循环的结果或许不过是几针,高层循环的结果会是一大块布。
侯世达定律:做事所花费的时间总是比你预期的要长,即使你的预期中考虑了侯世达定律。
六 意义在于何处
——音程增值的卡农
抽出的过程可能涉及到相当复杂的操作,以至于是你感到你放进去的信息比抽出的还多。
唱片和音乐之间是平凡同构的,因为存在唱片的每一刻痕都能和音乐精准地像,而DNA和表型则是异常同构。
一种观点认为,DNA离开环境毫无意义,另一种观点认为,即使离开了环境,一个来自生物体地DNA分子对起结构来说仍有一种“强制的内在逻辑”,不管怎样总能推导出它所带的信息。
任何消息都分三个层次:
- 框架消息
由信息携带者总体的结构特征隐含传递的
- 外在消息
解译内在消息的解码机制
- 内在消息
就是抽取发送人所要传递的意义
对艺术作品而言,努力传递风格也许是最重要的
一旦我们在某处发现一个非常规律的几何结构中“包裹着”非周期性晶体结构,那里就可能隐藏着一些内在信息。
在你能使用任何规则之前,你必须有另一个规则来告诉你如何使用这些规则。
智能喜爱模式化,厌恶随机性。
七 命题演算
——半音阶幻想曲,及互格
主要讲关于逻辑推导的基础,以及如何机械地使用递归和基础逻辑进行命题的演算
把两个真句子结合起来并不保险
规则清单:
- 联接规则:如果x和y是定理,那么<x$ \bigwedge $y>是个定理。
- 分隔规则:如果<x$ \bigwedge $y>是一个定理,那么x和y二者都是定理。
- 双弯号规则:”~~“这个串可以从任何定理中删除,也可以嵌入到任何定理中,只要所得的结果本身是良构串。
- 幻想规则:如果假定x是一个定理时能推导出y来,那么<x$ \rightarrow $y>是一个定理。
- 搬入规则”:在一个幻想里面,任何来自于“显示性”高一个层次的定理都可以拿进并使用。
- 分离规则:如果x和<x$ \rightarrow $y>都是定理,那么y是一个定理。。
- 易位规则: <x$ \rightarrow $y>与<y~$ \rightarrow $~x>是可以互换的。
- 德.摩根规则:<~x$ \bigwedge $~y>与~<x$ \bigvee $y>可以互换。
- 思维陀螺规则:<x$ \bigvee $y>与<~x$ \rightarrow $y>可以互换。(如果~x为真,则能推出y为真。若x,y都为真,什么都没有)
从某种角度看,命题演算是浪费时间的,因为它告诉我们的东西都微不足道。
有什么机械的方式来判断定理和非定理吗?
你永远无法维护你的推理模式,到了一定步骤就只能靠信仰了。——刘易斯.卡罗尔
一个人永远也不能给出一个最终的、绝对的证明,去阐明在某个系统中的一个证明是正确的。当然,一个人可以给出一个关于证明的证明,或者关于一个证明的证明的证明——但是,最外层的系统有效性总还是一个未经证明的假设,是凭我们的信仰来接收的
矛盾是在生活中各个领域中取得澄清和进步的一个主要源泉。
八 印符数论
——螃蟹卡农
本章主要是在构建一个推导系统,相比最开始的WUJ系统更为复杂。
“口味无须争辩”——拉丁谚语
印符数论(Typographical Number Theory)简称TNT
中间对皮亚诺五公设使用了之前神灯精灵进行了改写。改写后五条皮亚诺公设如下:
- 怪物是一个神怪;
- 每个怪物都有一个元(它也是一个神怪);
- 怪物不是任何神怪的元;
- 不同的神怪有不同的元;
- 如果怪物有X,并且每个神怪都把它的X递送给它的元,那么所有的神怪都得到X。
原皮亚诺五公设:
- 1是自然数;
- 每个确定的自然数都有一个确定的后继$a’$,$a’$也是自然数;
- 如果b,c都是a的后继,那b=c;
- 1不是任何自然的后继;
- 任意关于自然数的命题,如果证明了它对自然数1是对的,又假定它对自然数n为真时,可以证明它对n’ 也真,那么,命题对所有自然数都真。
九 无门与哥德尔
——一首无的奉献
讲了一些关于禅宗的公案,超越逻辑,带来混乱,最终至于无我的境界的
禅宗的信徒要寻求顿悟——就是一种“无我”状态。他不可以“执”于任何客体、思想或人。
也许正是幽默才使禅宗富于教益,我想如果你十分严肃地看待这些事,那你既会有所得也会有所失。
佛教禅宗地基本教条之一事:没有任何办法能刻画禅宗是什么。
很可能公案的目的恰恰就在于引起困惑,因为人的心智处于困惑状态时就会再某种程度上不合逻辑地运转,只有跳出逻辑,摆脱理论,人才能跃入顿悟境地。
禅宗反对二元的斗争
如果词语不好,思维也不好,那么什么是好的?这样问已经是彻头彻尾的二元论了。
一师因一僧问曰:“如何是道?”
师曰:“正眼前是道。”
“如何我不自见?”
“汝自虑故。”
“师知之否?”
师曰:“汝但见二分,言‘我不自见’,‘师见之’,汝目障矣。”
“无我无你,可得见否?”
“无我无你,谁欲见之?”
禅宗和尚拔对一个行将圆寂的门人写了一封信,信中说:“汝之无终之终,一似雪片溶于清气之中”。
它漂浮于堕界中,于没打出的嗝再一起,于没人读的故事中的人物在一起,(与山中无人观赏的花在一起)……
桶中无水,水中无月。
一旦对一个形式系统进行了哥德尔配数,结果是我们可以把对任一形式系统的研究转成数论工作。
十 描述的层次和计算机系统
——前奏曲
终于到了熟悉的计算机了,说了关于抽象的层次和编译器自举的情况
有一种比直接描述每处棋子的位置层次更高的描述,而大师就是以某种方式生成了这样一个棋局的心智表象。
十一 大脑和思维
——蚂蚁赋格
高层系统和底层系统之间应该存在中间系统,这是从低级到高级的关键,分子移动和风之间不存在中间系统,所以就没有产生智能。
整体论说“整体大于各部分之和”
简化论说“如果你理解了一个整体的各部分,以及把这些部分‘整合’起来的机制,那么你就理解了整个系统“。
无:通过废问这个问题,揭示出更广泛的真理,存在着某种更大的领域,使得整体论与简化论的解释都适合。
作为个体来看,即使每个蚂蚁的活动路线似乎是很随意的,然而就大量的蚂蚁来说,从这种乱糟糟的状态中,还是能看出存在着一些总的趋向。
这种层次太微观,当你从微观的角度进行思考时,你必然会漏掉更大规模上的现象。
在识别时好像感到有什么东西在你的脑海里”结晶“了。
结晶:在这个图像里,介质中无数微观的互不相干的活动缓慢地造成区域的一致性。
我们从电视屏幕感知到的不仅仅是点,还有组块。
对同一个脑的同一个状态来说,低层次的描述——面向神经原的——要变成高层次的描述——面向模块的。
昆虫的符号
在昆虫脑海中有的不是随机应变,而是写在基因中的if-then语句。
十二心智和思维
——英、法、德、中组曲
使用自想国,即将中国地图城市名字抹掉,自己给每个城市村庄添加名字。每个人的自想国都不相同。但是一些重要地方是相同的,同时如果比较不同人的心智也是难题,现在的知识图谱可能解决一些问题,可惜我了解不多。这一章作者也多次提到了另一位人工智能的大佬明斯基,果然还是绕不开这位大神。
心智和思维之间能彼此映射吗?
如何将思维相似的大脑联系起来——具体说就是:
- 所有可选符号的对应(符号是比神经元高一级的子系统,是模块的)。
- 符号触发模式的对应。
虽然别人和我们在一些重要方面有差异,但仍然在某些深入的和重要的方法和我们”相同“——这是我们智能的核心。
初见卢卡斯
意思悖论的出现是因为有意识物除了能意识到别的东西,还能意识到自身,并且的确不能看作是可分离的。
复杂程度经常引起质的不同。
产生新的心智有两种方法:传统的生孩子,和新的方法即建造一个非常非常复杂的系统。
十三 Bloop和Floop和Gloop
——咏叹调及其种种变奏
Bloop是有界循环(bounded loop),Floop是升级版(Free loop)可以进行有界循环和无界循环。当Floop进行求解时可能出现三种情况
- 程序结束,输出Yes
- 跳出封闭循环,输出No
- 未能跳出封闭循环,程序无法结束(应该输出No)
Gloop是去除限制的Floop,能对程序的状态是否结束进行判断,但遗憾的是Gloop只能是神话了
你没有看到明显的无穷,是因为它已在你把握的图像中被隐含地捕获了。
自然只是给我们提供大量现实,它们表面上杂乱无章,直到我们选择某种有意义的现象,而且把它们从特定的,关系不大的关系中抽象出来,只有那时它们才会展现出光彩夺目的真实结构。
在Floop可计算函数可以被分为两类:1)哪些能用有终止Floop程序计算的被称为”一般递归的“,2)那些只能用无终止Floop程序计算的被称为”部分递归的“
康托尔的对角线论证
“实数有无穷多个,因此显然不能列在一个有限长的登记表中。”
假设我们能给出无穷长的表,其中每一个正整数N对于于0和1之间的一个实数r(N)而且0和1之间的每一个实数都将出现在表中的某一个位置。设想表如下:
r(1):.141592653……
r(2):.333333333……
r(3):.718281828……
r(4):.414213562……
r(5):.500000000……
对角线上的1、3、8、2、0……用它们减去1(设0-1=9),得到一个数d:
0.02719……
这时,根据我们的构造方法有:
d的第一位不同于r(1)的第一位;
d的第二位不同于r(2)的第二位;
……等等
因此我们有
d不同于r(1);
d不同于r(2);
……等等。
就是说d不在表中。
十四 论TNT及有关系统中形式上不可判定的命题
——G弦上的咏叹调
主要讲哥德尔配数,证明对,哥德尔第二定理,超自然数,希尔伯特第十问题等,完全不懂,之后如果能了解一些相关的知识之后再反过来看吧 Orz
“由六个字组成”由六个字组成
十五 跳出系统
——生日大合唱哇哇哇乌啊乌啊乌啊……
假如一个TNT系统中存在矛盾G,那能否将G作为补丁加入到TNT公理中,从而解决矛盾呢?不行,因为TNT+G系统会产生新的矛盾G‘,再把G’加入又会有新的矛盾产生……对于系统的超越,可能真是一个神话,有人说就是看了GEB之后对所有关于meta(元)的东西都格外感兴趣,元分析,元游戏似乎都是一种高级的哲学。也许《鹿鼎记》也能算是金庸对他武侠的元分析,或者说解构。
哥德尔的论证的这种扰乱神智的可重复性,已经成为很多人——尤其是卢卡斯——的做战武器,想以此说明人类智能具有的某种难以捉摸,不可言状的特点。因此机械自动机——计算机——不能达到人类智能。
我们人类能否跳出自身——或者是,计算机程序是否能跳出自身呢?这仍是一个现代的神话。
广告和框架手法
一位著名专业演员做完了一个广告,摄影机还在对着他,他就明显地做出解除了任务地状态,沉浸于享用他刚刚宣传地那种产品地实际快乐中。
观众越是把一些次要地细节当作检验标准,广告商就迫得越急。
在禅宗里,我们也看到了这种对超出系统的概念的神往。
十六 自指和自复制
——一位烟民富于启发性的思想
副标题来自于抽烟的巴赫,这章也提到了另一位画家马格里特,画了一堆香烟雪茄相关的话,还有就是烟草花叶病毒。这章主要说的是自噬和自复制,说了很多DNA复制,中心法则相关的内容。并且企图将TNT系统和DNA复制系统进行同构。由其惊奇的是发现,十五种氨基酸的功能集和计算机的指令集极其相似。需要有一个翻译DNA的方式来帮助DNA的自复制。生命的起源可能是左脚踩右脚起飞的惊奇。这章看得不是很懂,中心法则大概还记得,懂了作者大意,细节有机会在来扣。
十七 丘奇、图灵、塔斯基及别的人
——的确该赞美螃蟹
如何在之前的系统不够强大的情况下,发展人工智能呢?拉玛奴衍这种天才而为经过多数学训练的人,给了灵感。能否从其他混乱的路,直觉的路研究出的系统与数学推导的系统有相同的功能,并且更强呢?图灵测试棒的地方在于不管你如何实现,只要你能骗过检测员就好
思维的每一个方面,都可以看成是从高级的层次上描述的一个位于较低层次、受某些简单的乃至形式的支配规则的系统。
数学家只与那些简单的、考究的形式系统的打交道,在那些系统中,一切东西都是有着极为清晰的定义,而大脑与此大相径庭。
想要了解大脑这样的复杂系统,唯一的方法是在越来越高的层次上对之组块,因而每一步都要损失一些严格性。
在现实生活的许多场合,演绎推理之所以不适用,并不是因为它会得到错误答案,而是因为它会得到过多的正确而无关的断言。
丘奇定理:没有一个切实可靠的方法总能区分开TNT的定理和非定理。
塔斯基-丘奇-图灵定理:没有一种切实可靠的方法总能区分开真数论语句和假数论语句。
丘奇-图灵论题,大众过程形式:假设有一种方法,一个有感知能力的生物可以根据它逐个把数分成两类。又假设这种方法总能在有穷的时间内得到结果,并且对给定的数它总能给出相同的结果。同时,还要假定这种方法可以通过语言由一个有感知能力的生物不走样地传递给另一个有感知的生物。那么存在一个有终止的Floop程序,它给出的答案恰好和这个有感知的生物所得的答案一样。
世上有一种奇怪的悖论效果:一件你认为不会促使人们轻信,而是会使易轻信的人变得开始怀疑的事,实际上却具有相反的效果。
人工智能论题:随着智能机的发展,它的基础机制会逐渐收敛于人类智能的基础机制。换句话说,一切智能都是同一主题下的变奏
十八 人工智能:回顾
——施德鲁,人设计的玩具
绕不开的图灵,说了九种图灵预测的反对意见。很有意思,里面的帕里与医生让我联想GAN,狗和肉骨头说的是最优化搜索的问题。里面还总结了几个大框架,机器翻译,博弈(跳棋,象棋,围棋等……),数学定理证明,计算机视觉,听觉,自然语言理解,自然语言生成,计算机创作(作诗,作画),类别,学习(参数调节,概念形成),现在计算机领域的研究似乎都没有逃出几十年前的划下的范围。
里面提到的塞缪尔跳棋程序,有必要一看,这似乎是搜索算法中比较经典的,它解决了跳棋问题,只是在国际象棋中效果不好,这或许对之后的蒙特卡洛搜索算法也有启示。
对于图灵测试,我们假定最好的策略就是设法提供那种人会很自然地给出的答案。
图灵假设的九种反对意见
- 神学上的: 思维是上帝给男人和女人的,没有给动物和机器,所以机器不能有思维。
- 鸵鸟式的: 机器思维的后果将很可怕,让我们希望并且相信它们不能做到吧。
- 数学上的: 卢卡斯的论点
- 基于意识的: 除非机器有自己的思想和情感写出一首诗或者一只曲,否则我们就不能说机器等于大脑
- 基于各种缺陷的: “就算你能造出一台机器做出你所提到的那些事,你也绝不可能提出一台能做到X的机器”,X包括善良、机智、优美、友好……
- 洛夫莱斯的反对意见: 分析机并不自称能创造任何事,它能做任何我们知道怎么命令它的事。
- 基于神经连续性的论点: 神经状态肯定不是一台离散状态的机器,我们不能指望用一个离散状态系统来模拟神经元系统的行为。
- 基于行为非形式化的: “如果每个人都有一个确定的指导规则集来控制他的生活,那他就无异于机器了,但并不存在这种规则,因此人也就不是机器。”
- 基于超感官知觉的: 假设我们进行模拟游戏,两个被问者一个是能接受心灵感应的,另一个是机器人。询问人可以问:“我右手里这张扑克牌什么颜色?”那个有心灵感应的人400次询问中对了130次,机器人随机猜测也许对了103次,这样,询问人就能做正确判断了。
第九个问题再图灵论文被重印时删除了,这点特别有意思,图灵也不想承认真的有特异功能,但他的求实精神要求他接受他认为是强有力地支持了超感官知觉的统计证据。
塞谬尔德跳棋程序:同时使用动态(超前搜索)和静态(非超前搜索)方法。将动态搜索所得的知识被部分编码于静态估值函数的参数中了。基本想法就是把复杂的动态估值方法“压缩”到简单得多也有效得多的静态估值函数中来。
棋艺高超的棋手在选择棋步时所依赖的心智过程,往往连他们本人也无法全部揭示——他们在使用自己的直觉。现在(1979年)还没人知道怎么揭示自己的所有直觉。
你若是对某个东西感到厌倦,这往往不是由于你穷尽了它所有可能的行为,而是你发现了包含其全部行为的空间的界限。
狗和肉骨头
一只叫山迪的狗,看到栅栏外有一个肉骨头,它有两种方法
- (a)跑到栅栏前;(b)通过它;(c)跑向肉骨头
- (a)跑到栅栏门;(b)通过门;(c)跑向肉骨头
第一个方法的第二个子问题太难了,狗无法解决,而第二个方法第一步看起来是把问题复杂化
一切都取决于如何表示“问题空间”——也就是说,把什么看成是对问题的“简化”(即朝总目标的行动),把什么看成是对问题的“复杂化”(即背离总目标的行动)
对于最优化问题的解法:
- 试着以某种随机的方式离开目标,希望能发现隐藏的门。
- 设法发现一个新的问题表示空间。
第一种方法似乎太慢,而第二种方法似乎太难(现在的基因算法等是指就是好一些的第一种方法,棘轮法通过隔一次稍微调节一下目标函数,是用的第二种解法)
十九 人工智能:展望
——对实
哪些事是我们以为差点发生的,哪些是不会发生的呢?这种对现实的其他情况的想象也许是人智能的来源。也是一切美好的源头。
双目独眼龙
虚拟的比赛在月器上进行时的情景
如果心智在一个否定句中除了晦暗的障碍以外什么都看不到,那么该是多平淡乏味啊!一个活生生的心智总能发现通往可能性世界的窗口。
试想,如果我们没有这种滑出真实世界、进入“假如”世界中的创造能力,那么我们的精神生活将是何等的贫乏啊。
从数学中借助“常量”,“参量”,“变量”来便是事情条件可变的程度。
很难设想一个通用算法,能从相互碰撞的符号中构造出有意义的新符号来。就像两本书的词重新随机组合能得到另一本书的可能性一样。
归根结底,在严谨的卡农艺术中,为了达到典雅和优美,偶尔也难免出现不完全的模拟。
如果能有如此功能的程序必须得自己走进世界,在纷繁的生活中抗争,并每时每刻体验到来自生活的感受,它必须懂得暗夜里凉风所带来的喜悦与孤独,懂得对于带来温暖爱抚的手掌的渴望,懂得遥远异地的不可企及,还要能体验到一个人死去后引起的心碎和升华。它必须明了放弃与厌世、悲伤和失望、决心和胜利、虔诚与敬畏。
二十 怪圈,或缠结的层次结构
——树懒卡农
怪圈的出现,可能是在怪圈之外有一个看不见的不受干扰的层次造成的这个情况。艾舍尔的《画手》就是作者画了两只相互画着对方的手
一旦你无法跳出系统寻求更高的权威时,那唯一的办法就是求助于哪些看上去没有用规则定义清楚的力量,而它们才是最高层次规则的唯一来源——这就是底层规则。在找不到更高级的法院来裁判时,求助于社会普遍反应也是好办法。
“寻找关于自我的知识就像踏上了这样一条旅途……它并非无处不通,它不能被描绘在任何图纸上,它永无尽头,它不可描述。”
与主体-客体二分法密切相关的是符号-对象二分法,这已经由路德维希.维特根斯坦深入地讨论过了。
谁也没办法抑制好奇心产生地疑虑。
艾舍尔《画廊》中中心有一个“瑕疵点”写着他的签名,虽然看着像一个缺陷,但这个缺陷是在我们的期望之中的,因为艾舍尔无法完成那一部分,除非他违背他作画时的一贯规律。
——六部无插入赋格
螃蟹的客人 查尔斯.巴比奇
