kdtree算法
Intro
kd树(k-dimensional树的简称),是一种分割k维数据空间的数据结构。可以理解
为多维数据的二叉搜索树。这里包括两个问题如何建树,如何搜索
如何建树
- 建立根节点;
- 选取方差最大的特征作为分割特征;
- 选择该特征的中位数作为分割点;
- 将数据集中该特征小于中位数的传递给根节点的左儿子,大于中位数的传递给根节点的右儿子;
- 递归执行步骤2-4,直到所有数据都被建立到KD Tree的节点上为止。
为什么选择方差最大的特征作为分割特征
因为方差大,数据相对“分散”,选取该特征来对数据集进行分割,数据散得更“开”一些。
为什么选中位数作为分割点
让左子树和右子树的数据数量一致,使建立的树更平衡,树越平衡搜索的时间也就是越少
如何搜索
- 从根节点开始,根据目标在分割特征中是否小于或大于当前节点,向左或向右移动。
- 一旦算法到达叶节点,它就将节点保存为“当前最佳”。
- 回溯,即从叶节点再返回到根节点 (使用root=root.father)
- 如果当前节点比当前最佳节点更接近,那么它就成为当前最好的。回溯的过程中也计算距离
- 如果目标距离当前节点的父节点所在的数据集分割为两份的超平面的距离更接近,说明当前节点的兄弟节点所在的子树有可能包
含更近的点。因此需要对这个兄弟节点设为根节点递归执行1-4步。(使用队列方法,对兄弟节点的执行为将兄弟节点和兄弟节点对应
找到的叶子节点,加入到队列中,队列为空后返回的即为最接近的节点)
第五步什么意思
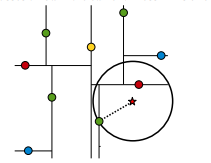
如图,黄->红->绿->蓝分别代表树第1,2,3,4层的分割点,星表示目标点,绿点为第2步找到的最佳点。
在判断其他子节点空间中是否有可能有距离查询点更近的数据点时,做法是以查询点为圆心,以当前的最近距离为半径画圆,这个圆称为候选超球(candidate hypersphere),如果圆与回溯点的轴相交(计算超平面距离与当前节点到目标节点的距离,如果前者小于后者就相交),则需要将轴另一边的节点(即当前节点的兄弟节点)都放到回溯队列里面来。
代码地址:
GitHub
完整代码如下1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155class Node:
def __init__(self):
self.father = None
self.left = None
self.right = None
self.feature = None
self.split = None
def __str__(self):
return "feature: {}, split: {}".format(str(self.feature), str(self.split))
# 获取兄弟节点的值,使用装饰器将方法当作属性调用
def brother(self):
if not self.father:
return None
elif self.father.left is self:
return self.father.right
else:
return self.father.left
class KDTree:
def __init__(self):
self.root = Node()
# 查看节点值
def __str__(self):
ret = []
i = 0
que = [(self.root, -1)]
while que:
node, idx_father = que.pop(0)
ret.append("{} -> {}: {}".format(idx_father, i, node))
if node.left:
que.append((node.left, i))
if node.right:
que.append((node.right, i))
i += 1
return "\n".join(ret)
def _get_median_idx(self, X, idxs, feature):
n = len(idxs)
k = n // 2
# 找到方差最大
col = map(lambda i: (i, X[i][feature]), idxs)
sorted_idxs = map(lambda x: x[0], sorted(col, key=lambda x: x[1]))
median_idx = list(sorted_idxs)[k]
return median_idx
def _get_variance(self, X, idxs, feature):
n = len(idxs)
col_sum = col_sum_sqr = 0
for idx in idxs:
xi = X[idx][feature]
col_sum += xi
col_sum_sqr += xi ** 2
# float 不能进行位运算 **2 不能写成<<1
return col_sum_sqr / n - (col_sum / n) ** 2
# 选取方差最大的特征作为分割点特征
def _choose_feature(self, X, idxs):
m = len(X[0])
variances = map(lambda j: (
j, self._get_variance(X, idxs, j)), range(m))
return max(variances, key=lambda x: x[1])[0]
# 将大于和小于中位数的元素分别放入两个列表中
def _split_feature(self, X, idxs, feature, median_idx):
idxs_split = [[], []]
split_val = X[median_idx][feature]
for idx in idxs:
if idx == median_idx:
continue
xi = X[idx][feature]
if xi < split_val:
idxs_split[0].append(idx)
else:
idxs_split[1].append(idx)
return idxs_split
def build_tree(self, X, y):
nd = self.root
idxs = range(len(X))
que = [(nd, idxs)]
while que:
nd, idxs = que.pop(0)
n = len(idxs)
# Stop split if there is only one element in this node
if n == 1:
nd.split = (X[idxs[0]], y[idxs[0]])
continue
# Split
feature = self._choose_feature(X, idxs)
median_idx = self._get_median_idx(X, idxs, feature)
idxs_left, idxs_right = self._split_feature(
X, idxs, feature, median_idx)
# Update properties of current node
nd.feature = feature
nd.split = (X[median_idx], y[median_idx])
# Put children of current node in que
if idxs_left != []:
nd.left = Node()
nd.left.father = nd
que.append((nd.left, idxs_left))
if idxs_right != []:
nd.right = Node()
nd.right.father = nd
que.append((nd.right, idxs_right))
def _search(self, Xi, nd):
while nd.left or nd.right:
if not nd.left:
nd = nd.right
elif not nd.right:
nd = nd.left
else:
if Xi[nd.feature] < nd.split[0][nd.feature]:
nd = nd.left
else:
nd = nd.right
return nd
def _get_eu_dist(self, Xi, nd):
X0 = nd.split[0]
return get_euclidean_distance(Xi, X0)
# 计算超平面距离
def _get_hyper_plane_dist(self, Xi, nd):
j = nd.feature
X0 = nd.split[0]
return abs(Xi[j] - X0[j])
def nearest_neighbour_search(self, Xi):
dist_best = float('inf')
nd_best = self._search(Xi, self.root)
que = [(self.root, nd_best)]
while que:
nd_root, nd_cur = que.pop(0)
dist = self._get_eu_dist(Xi, nd_root)
if dist < dist_best:
dist_best, nd_best = dist, nd_root
while nd_cur is not nd_root:
dist = self._get_eu_dist(Xi, nd_cur)
# Update best node, distance and visit flag.
if dist < dist_best:
dist_best, nd_best = dist, nd_cur
# If it's necessary to visit brother node.
if nd_cur.brother and dist_best > \
self._get_hyper_plane_dist(Xi, nd_cur.father):
_nd_best = self._search(Xi, nd_cur.brother)
que.append((nd_cur.brother, _nd_best))
# Back track.
nd_cur = nd_cur.father
return nd_best
参考博客
https://zhuanlan.zhihu.com/p/45346117
https://blog.csdn.net/silangquan/article/details/41483689